O
Problema do Caixeiro Viajante
Marco
Ganhoto (*)
O
Problema do Caixeiro Viajante - PCV (Traveling
Salesman Problem - TSP) é um dos mais tradicionais
e conhecidos problemas de programação
matemática. O objetivo do PCV é
encontrar, em um grafo G=(V,A), o circuito
hamiltoniano de menor custo.
Um
grafo, numa definição bem simples,
é um conjunto de Vértices e Arestas.
Os vértices (ou nós) são pontos
que podem representar cidades, depósitos, postos
de trabalho ou atendimento. Já as arestas são
linhas que conectam os vértices, podendo representar
ruas ou estradas, por exemplo. Um circuito
hamiltoniano é um passeio que percorre
todos os vértices de um grafo e retorna ao
vértice origem (início do passeio),
passando por cada vértice apenas uma vez.
Tal
passeio recebe esse nome devido a Willian Rowan
Hamilton que, em 1857, propôs um jogo que
denominou Around the World. O jogo foi elaborado sobre
um dodecaedro em que cada vértice estava associado
a uma cidade importante da época. O objetivo
era encontrar uma rota através dos vértices
do dodecaedro que iniciasse e terminasse em uma mesma
cidade sem nunca repetir uma visita.
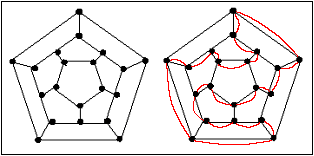
Figura 1
Uma
das soluções do jogo está apresentada
na Figura 1. Note que o "jogador" visita,
(entra e sai em), todas as cidades e retorna ao vértice
inicial. Hamilton não foi o primeiro a propor
esse problema, mas o seu jogo ajudou a divulgá-lo.
Modernamente, a primeira menção conhecida
do problema é devida a Hassler Whitney em 1934
em um trabalho na Princeton University.
O
Problema do Caixeiro Viajante é importante
devido a pelo menos três de suas características:
grande aplicação prática, grande
relação com outros modelos e grande
dificuldade de solução exata. Em suas
diversas versões, o PCV está presente
em inúmeros problemas práticos, como
por exemplo:
Para
ilustrar melhor algumas dessas aplicações,
veremos a seguir 3 simulações geradas
a partir de um projeto realizado numa disciplina de
um curso de pós-graduação. No
primeiro exemplo, imagine que um empresário
precisa visitar as filiais da sua empresa que estão
localizadas nas capitais dos estados e no Distrito
Federal. É um exemplo simples, mas existem
várias soluções para a questão;
por exemplo, o empresário poderia sair de São
Paulo com destino a Manaus e na seqüência
seguir para Porto Alegre e depois para Belém.
Certamente este não seria um bom início
pois estaríamos percorrendo grandes distâncias
que encarecem o passeio. A idéia é encontrar
um circuito hamiltoniano que minimize os custos (neste
caso a distância a ser percorrida). Uma sugestão
seguramente melhor está ilustrada na figura
2.
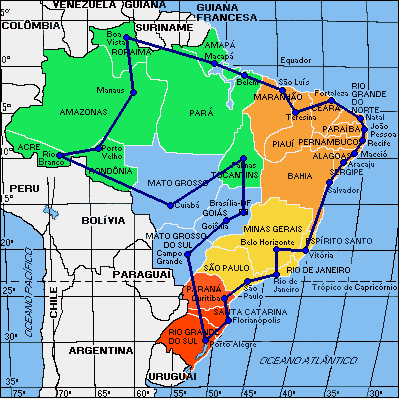
Figura 2
A
simulação mostrada na Figura 3 ilustra
um circuito hamiltoniano a ser percorrido por uma
ferramenta responsável pela perfuração
de uma placa de circuito impresso. O circuito impresso
em questão é bem simples, mas existem
inúmeros outros circuitos muito mais complexos
que precisam ser perfurados e soldados geralmente
em grande quantidade. Por isso o PCV é utilizado
para tentar encontrar soluções que diminuam
o tempo do processo.
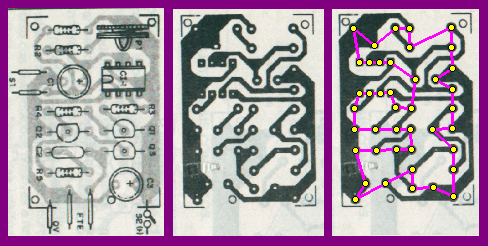
Figura 3
No
exemplo de número 3, temos um grafo com 50
pontos distribuídos num mapa da Grande São
Paulo. Imagine por exemplo que o "caixeiro"
precisa percorrer todos estes pontos com um helicóptero
levando vacinas para serem distribuídas. Novamente
existem muitas soluções para o problema,
dentre elas a mostrada na Figura 4.
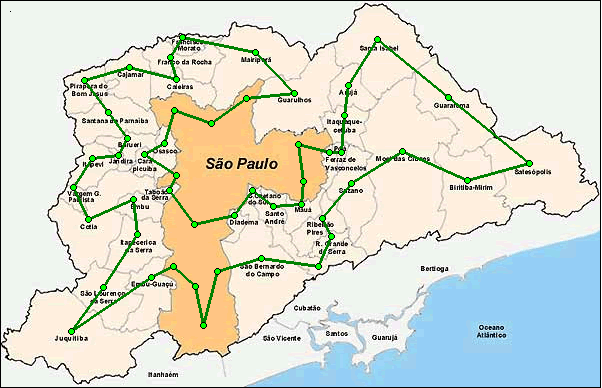
Figura 4
O
PCV pertence a classe de problemas considerados difíceis
ou intratáveis. A busca de uma solução
ótima pode "custar caro", pois a
medida que aumentamos o número de vértices
o tempo para a resolução do problema
aumenta de forma gritante, tornando as vezes a resolução
inviável para os computadores atuais. Para
problemas difíceis, são utilizadas algumas
técnicas para tentar resolver o problema em
tempo hábil como por exemplo a elaboração
de Algoritmos de Aproximação.
Algoritmos
de aproximação são aqueles que
apresentam uma solução correta com a
garantia de que esta solução está
dentro de uma determinada porcentagem da solução
ótima. Fazendo uma análise do pior caso
e do melhor caso que o algoritmo pode produzir, é
possível avaliar sua complexidade e a proximidade
das suas soluções em relação
à aquela que é ótima. Com o uso
de algoritmos de aproximação é
possível encontrar, para problemas difíceis,
soluções de boa qualidade em tempo computacional
aceitável.
Na
página do professor Flávio Keidi Miyazawa
(http://www.ic.unicamp.br/~fkm/)
estão disponíveis diversas informações
sobre "Otimização",
além de links para vários assuntos relacionados
a "Teoria da Computação".
Nela também podemos encontrar um link para
uma página que fornece diversas informações
sobre o TSP (http://www.math.princeton.edu/tsp/index.html),
além da resolução de uma instância
de 15112 cidades (http://www.math.princeton.edu/tsp/d15sol/d15map.html);
vale a pena visitar!
